My Solutions for LG Dream Code 2025
Recently, LG Electronics has recently been holding this Dream Code competition for graduating or recently graduated students in Vietnam. They just held one this year on June 14th and I got the chance of participating in it. Unfortunately, I didn’t make it to top 50 (probably because I was an hour late to the competition). I did manage to complete all the challenges, though my solutions aren’t the most efficient. Here are my solutions.
I’m going to paraphrase the problem to the essential parts because it’s pretty long.
1st problem: Toy Race
This problem gives us 4 inputs: 3 ints (N, X, Y) and 1 int array (V). There’s an additional variable in the problem called Z too.
Nrepresents the label of our car.Xrepresents the length of the race track.Yrepresents the maximum speed our car can handle.- Each variable in
Vrepresents the speed each car will move at. The index of the variable is the label of the car. So if my labelN = 3then the 3rd variable inVis the speed of our car. Zrepresents the speed that our car will boost to for 1 second at the start of the race. So our car will travel atZfor 1 second at the beginning of the race then it will go atV[N]for the rest of the race.
The goal here is to find the minimum Z value that would allow us to win the race and output that value to stdout. If we can win the race without using the booster, we output 0. If we can’t win the race even if we use the booster at the maximum value Y, we output -1.
Below is a sample input for this problem:
5
3 12 11
3 2 1
3 12 9
3 2 1
3 12 10
3 4 5
3 80 80
80 60 70
3 80 80
70 50 60
The first line is the number of test cases called T. Each cases contain 2 lines. The 1st line contains N, X, and Y. The 2nd line contains the values for V. All of these values are separated by a space.
Firstly, since this receives input via stdin, I builted this function for reading the data into variables using the sys library and iter() in our program:
import sys
def main():
data = sys.stdin.read().strip().split()
it = iter(data)
T = int(next(it))
for i in range(T):
N = int(next(it))
X = int(next(it))
Y = int(next(it))
V = [int(next(it)) for i in range(N)]
print(solve(N, X, Y, V))
if __name__ == "__main__":
main()
Now we just need to implement the solve() function. I’ll show the code first then I’ll explain what it does.
def solve(label, track_len, max_boost, V):
speeds = V[:]
others_time = []
my_vel = speeds.pop(label - 1)
my_time = track_len / my_vel
# calc other's time
for v in speeds:
others_time.append(track_len / v)
if my_time < min(others_time):
return 0
# calc optimal Z
for v in range(my_vel + 1, max_boost + 1):
boosted_dist = track_len - v
boosted_time = (boosted_dist / my_vel) + 1
if boosted_time < min(others_time):
return v
return -1
First, I copied the V array into speeds because I’m going to perform some array manipulation. This doesn’t really affect anything about this program because it’s so short and specific, it’s just standard practice. Next I grabbed our car’s velocity value into my_vel and calculate the time it would take us to finish the race and store it into my_time.
Next, I calculated the values of the other cars’ race times and store it into others_time. If my_time is shorter than the minimum of others_time, we don’t need to use the booster at all. Otherwise, we calculate the optimal Z.
For calculating the optimal Z, I iterate through each Z values from my_vel + 1 to Y. Because the speed is measured in m/s and the track is in meters and the boost time is only 1 second, we can subtract the boost value from the length of the track to and add 1 second to our time, resulting in a new track length. On the new track length, we can calculate how much time it’d take us to finish that track and add 1 second to that time, giving us the our boosted time.
Finally, we use the same compare logic as before. If it is the shortest time, we return the current Z value, else if no Z value is found, we return -1. This was a pretty simple problem.
2nd problem: String Reversal
This problem gives us an array S with N number of strings. We are also given a function that reverse the string’s character order. We need to find the “reversal string” that would make the array lexicographically sorted. The reversal string is a bitmask that specifies which string in the array to reverse.
For example: An array S = ["ABC", "XC", "DZ"]. There are multiple different reversal strings that would make S lexicographically sorted.
001would reverse “DZ” to “ZD”, which would makeSlexicographically sorted.010would reverse “XC” to “CX”, which would also makeSlexicographically sorted
This is just 2 strings that would work, there are more that would also work for this particular S. The goal is to find a minimum reversal string that would make S lexicographically sorted. So as for the previous example, the output of S = ["ABC", "XC", "DZ"] would be 001 because it’s the smallest binary that would sort S.
Below is a sample input for this problem:
2
3
ABC
ABD
XY
3
ABC
XC
DZ
The first number is the number of test cases T. Each test cases will start with a number N. N is the length of the array S. Following that number are the strings inside the array S. The strings are only uppercase English letter.
Firstly, we need to read the data into our program:
import sys
def main():
data = sys.stdin.read().strip().split()
it = iter(data)
T = int(next(it))
for i in range(T):
N = int(next(it))
S = [next(it) for i in range(N)]
print(solve(N, S))
if __name__ == "__main__":
main()
We’ll brute-force this problem first, then optimize this program later. Firstly, we need to implement a function that reverses string as it’s an integral part of the problem. This is pretty simple to do in Python, it’s just 1 line:
def rev_str(string):
return string[::-1]
We’ll need some more helper functions. We need a function that checks whether S is lexicographically sorted or not and a function that translate the reversal string into indices in S that needs to be reversed. The 1st one is pretty simple to implement in Python, we just use sorted(). The 2nd one is also pretty simple, just check for the character ‘1’ and return the indices in an array.
def check_lex_order(str_arr):
return str_arr == sorted(str_arr)
def get_rev_indices(string):
indices = []
for i, c in enumerate(string):
if c == '1':
indices.append(i)
return indices
There’s also another helper function that I made called bump(). This just increases the reverse string like a binary number.
def bump(bin_str):
length = len(bin_str)
n = int(bin_str, 2) + 1
n %= (1 << length)
return format(n, f'0{length}b')
Now we can put this together and create a solve() function:
def solve(arr_len, str_arr):
reversal_str = "0" * arr_len
while True:
if check_lex_order(str_arr):
break
reversal_str = bump(reversal_str)
indices = get_rev_indices(reversal_str)
for idx in indices:
str_arr[idx] = rev_str(str_arr[idx])
return reversal_str
For this function, we first initialize the reversal string with zeroes. Next, we enter a loop that will keep looking for the correct reversal string. We check if S is in order, if yes then we break out of the loop. Next, we bump the reversal string to the next one, get the strings indices then reverse the strings in S at those indices.
This is a super simple brute-force approach. However, this did not meet the time limit as it was too slow. So I had to go back to the drawing board and come up with a better solution.
I landed on this 2-state dynamic programming approach:
def solve(arr_len, str_arr):
A = [[s, rev_str(s)] for s in str_arr]
dp = [[None, None] for i in range(arr_len)]
dp[0][0] = "0"
dp[0][1] = "1"
for i in range(1, arr_len):
for r in (0, 1):
best = None
for prev in (0, 1):
prev_bits = dp[i - 1][prev]
if prev_bits is None:
continue
if A[i - 1][prev] <= A[i][r]:
cand = prev_bits + str(r)
if best is None or cand < best:
best = cand
dp[i][r] = best
final0, final1 = dp[arr_len - 1]
if final0 is None:
return final1
if final1 is None:
return final0
return min(final0, final1)
A is a 2D array that holds the precomputed reversed string for each string in S. dp is the DP table for holding the smallest reversal string that sorts S lexicographically. We also initialize the dp table with 2 possible direction: reversing the first string or not reversing the first string. Each subsequent element of the dp table will be built on top of this initialization. The idea is the algorithm will search for the first reversal string with “0” that keeps the current string and the previous string in lexical order. If it can’t do that, it will move to using the reversed version of that string.
The outermost loop is the main gear of this function. We loop over each string pairs. The 1st inner loop loops over each of the bit choices for the current string. The 2nd inner loop loops over each bit choices for the previous string.
We check if the previous bit is none or not, if yes then it’s not a valid bit and we skip it. Else, we first check if the previous string is in lexical order with the current string. If this condition is satisfied, we form a new candidate for the reversal string. We store the candidate in the dp table.
The last element of the dp table contains the final reversal string. We just grab which ever one that isn’t none and return it. If both are not none then we just return which ever string is smaller.
This is much faster than the brute-force approach. In the brute-force approach, worst case scenario, we loop through all of the reversal string, and perform reversal on all of them to check. I calculated check_lex_order() to be O(NS log N) with S being the length of the string, get_rev_indices() to be O(N), and the inner loop in solve() to be O(N), meaning we reverse all the strings in the array. This gives us a time complexity of O(NS log N + 2N).
The 2-state DP approach is O(N * 4) because we only do N iteration in the outermost loop with the 2 inner loops doing at most 2 iteration each. Probably not the most efficient solution to this problem but it’s good enough for me.
3rd problem: Good Node-subsets
This problem is a tree problem. We are given a tree with N nodes, labeled 1 to N. We are also given 2 vectors: p and v. p holds the parent node of each node, with p[i] = 0 being the root node. v holds the integer value of each node.
For example: Given N = 6, p = [0, 1, 1, 3, 3, 3], and v = [30, 15, 10, 20, 15, 18], we can draw this tree out:
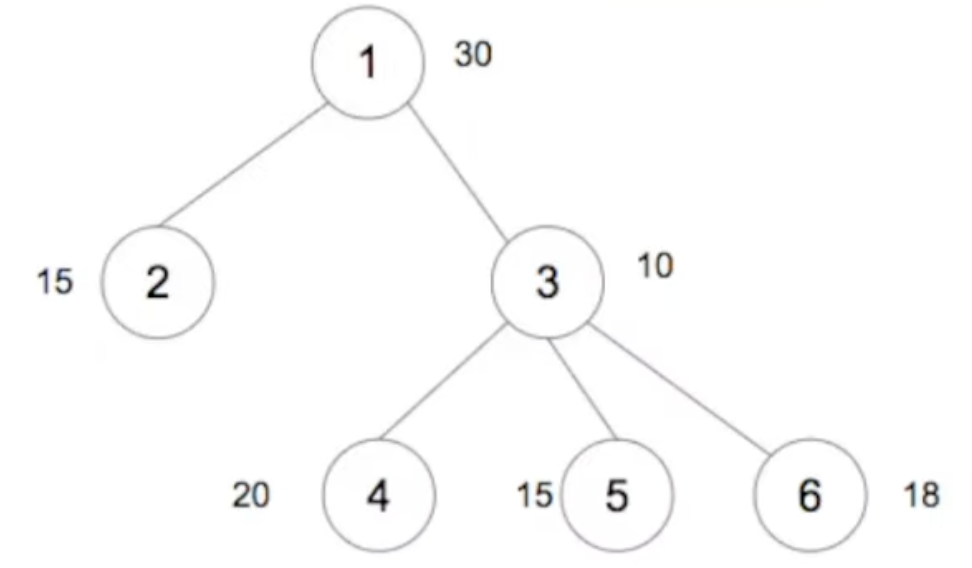
For a node-subset S to be a “good” node-subset, it needs to satisfies these 2 conditions:
- If a node is in
S, its parents and children node cannot be inS. - If a non-leaf node is not in
S, at least 1 of its children must be inS.
So for our above example tree, The following node-subsets are “good”:
S = [3]S = [1, 4, 6]S = [1, 4]S = [2, 3]
Below is a sample input for this problem:
5
6
30 15 10 20 15 18
0 1 1 3 3 3
6
1 120 100 10 20 30
0 1 1 3 3 3
6
100 8 5 -20 -30 15
0 1 1 3 3 3
5
-1 -2 -3 -4 -5
2 3 4 5 0
2
-2022 2022
0 1
The first line of the input is the test case T. Each test case has 3 lines. The first line of the test case is the number of nodes in the tree N. The second line is the v array with the integer values for each node. The third line is the p array, indicating the structure of the tree.
The objective here is for us to find the “good” node-subset that yields the highest sum value of each node in the node-subset. For example, in our above example tree, S = [1, 4, 5, 6] yields the highest sum value, 83, out of all the “good” node-subsets for that tree.
Firstly, we need to read the data into our program:
def main():
data = sys.stdin.read().strip().split()
it = iter(data)
T = int(next(it))
for i in range(T):
N = int(next(it))
v = [int(next(it)) for i in range(N)]
p = [int(next(it)) for i in range(N)]
print(solve(N, v, p))
if __name__ == "__main__":
main()
Let’s do the same thing, we check the brute-force approach, then check the DP approach. Let’s see the solve() function for the brute-force approach:
def build_tree(num_nodes, parents):
tree_list = [[] for i in range(num_nodes)]
# build tree list based on parents array
for i in range(num_nodes):
par = parents[i]
if par > 0:
tree_list[par - 1].append(i)
return tree_list
def solve(num_nodes, vals, parents):
tree_list = build_tree(num_nodes, parents)
best = -10**42
# bitmask for choosing nodes
for mask in range(1 << num_nodes):
chosen = [(mask >> i) & 1 for i in range(num_nodes)]
valid = True
# condition 1: no adjacent nodes chosen
for i in range(num_nodes):
if chosen[i]:
par = parents[i]
# node is not root node and its parent node is chosen
if par > 0 and chosen[par - 1]:
valid = False
break
if not valid:
continue
# condition 2: every unchosen node has at least 1 chosen child
for i in range(num_nodes):
# node is not chosen and node is not leaf node
if not chosen[i] and tree_list[i]:
# if none of the node's children are chosen
if not any(chosen[j] for j in tree_list[i]):
valid = False
break
if not valid:
continue
# calc score of valid subset
total = 0
for i in range(num_nodes):
if chosen[i]:
total += vals[i]
best = max(best, total)
return best
Because this is a tree problem, I converted the input into an adjacency list representation for ease of processing. I used a bitmask with N bits for choosing the node and turned the mask into a binary array with the length N. This mask means we try every possible combinations of node-subset possible. valid will hold the status of the subset.
There are 2 conditions that we need to check here. Let’s go through each of the condition check:
- Condition 1: For each chosen node, root nodes and nodes whose parent is also chosen violates condition 1.
- Condition 2: For each non-chosen non-leaf node, we check if none of its children are in the chosen array. If yes then it violates condition 2.
Finally, we calculate the score of the node-subset with best as the placeholder value. This approach is very slow, we used 3 loops, each with O(N) as the worst case scenario. Not to mention our bitmask enumeration loop too, which has a time complexity of O(B), with B being the number of bits in N. The build_tree() function also has a time complexity of O(N) too. So the time complexity of this algorithm as a whole is O(B4N). This is inefficent and it did not meet the time limit.
Let’s move onto the DP approach:
from collections import defaultdict
def solve(num_nodes, vals, parents):
tree = defaultdict(list)
root = -1
for i in range(num_nodes):
if parents[i] == 0:
root = i
else:
tree[parents[i] - 1].append(i)
# dp[node][0]: not selected, dp[node][1]: selected
dp = [[0, 0] for i in range(num_nodes)]
def dfs(node):
total_when_not_taken = 0
gain_if_take = vals[node] # if take node, can't take its children
child_selected_at_least_once = False
max_child_diff = float('-inf')
for v in tree[node]:
dfs(v)
# if take node, can't take its children
gain_if_take += dp[v][0]
# if don't take node, children can be taken (or no)
total_when_not_taken += max(dp[v][0], dp[v][1])
if dp[v][1] > dp[v][0]:
child_selected_at_least_once = True
max_child_diff = max(max_child_diff, dp[v][1] - dp[v][0])
# if node not taken and none of its children are taken, must take at least one
if not child_selected_at_least_once and tree[node]:
total_when_not_taken += max_child_diff
dp[node][0] = total_when_not_taken
dp[node][1] = gain_if_take
dfs(root)
return max(dp[root][0], dp[root][1])
This is also a 2-state DP approach. I ended up switching to building my adjacency list representation with defaultdict since it’s easier to build a DFS algorithm for this. We also initialize a dp table for each node. The 2 states in this table represents the total of the subset when not selecting and selecting the node, respectively.
Next, we do a post-order DFS. For each node, we recurse on all children v, so that dp[v][0] and dp[v][1] are computed before combining at dp[node]. After we visited all the child nodes, we set dp[node][0] and dp[node][1]. The final result will be stored in dp[root].
Within the DFS, if we take a particular node (dp[node][1]), we can’t take its children anymore. So we can only select dp[v][0], which is the “not select” state for the child node. gain_if_take holds the current node’s value plus the sum of its children in the “not select” state. If we don’t take a particular node (dp[node][0]), we have to take at least 1 of its children. We can optionally select the child nodes or not, depending on which option yields the highest result and this is summed into total_when_not_taken. However, we need to ensure that we’ll select at least 1 child node, which is expressed through the comparison dp[v][1] > dp[v][0] for some child nodes. If none of the child node is selected, we have to force select one. To minimize the loss of gain in this case, we pick the child node with the highest dp[v][1] - dp[v][0] and track it in max_child_diff. Because dp[v][1] and dp[v][0] holds the cummulative value of the calculation up to that node, taking the difference between the 2 give us the value of the child node that is force selected.
After we finish looping through the child nodes, if the current node is not taken and none of its child nodes are chosen, we force select a child by adding max_child_diff. If the node is a leaf node, we don’t have to add anything.
Finally, the final score is stored in the root node states, so we just take it directly from there and return it. This 2-state DFS DP algorithm will visit each node exactly once so the time complexity for this is linear (O(N)).
4th problem: Hiking
This is a graph problem. My (definitely not) favorite type of problems.
We are given 2 mountains: Mt. East and Mt. West, which I’ll just call East and West. East has n trails, the lengths of which are stored in an array called A. West has m trails, the lengths of which are stored in an array called B. Each trail begins and end at the same place, the entrance of its mountain. The entrances of the 2 mountains are connected by a bridge with the length of x.
Below is an example of a map of the 2 mountains with its trails and the bridge. The square indicates the entrance of East and the circle indicates the entrance of West.
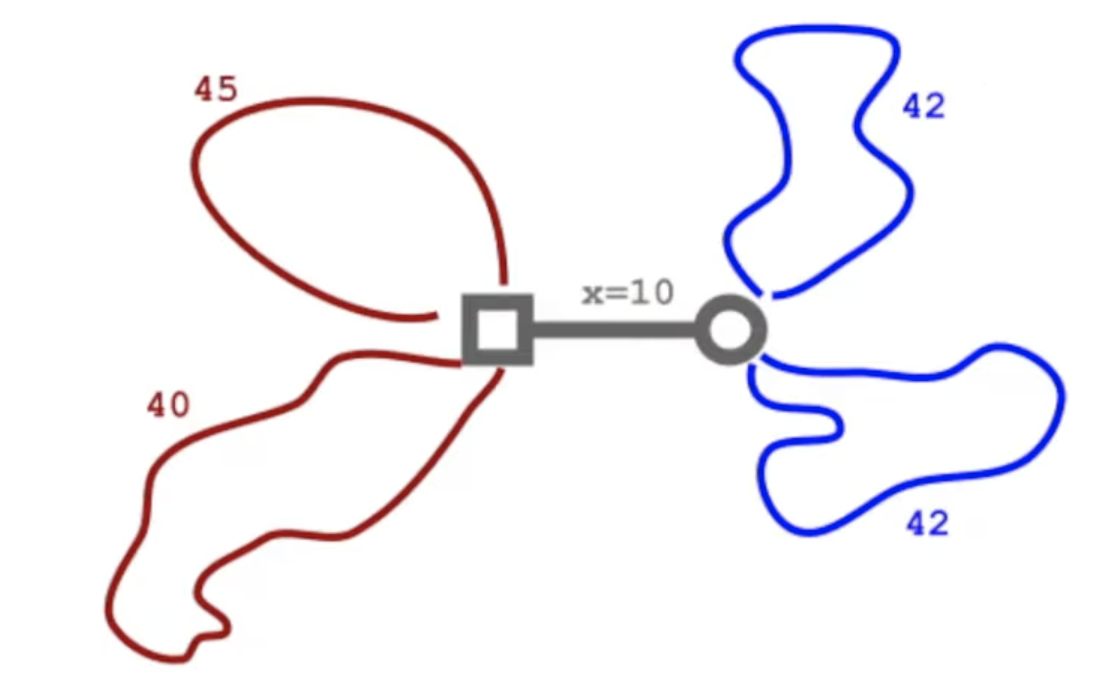
A hiking route needs to satisfy these conditions:
- The route’s length must be at least
Cand at mostDlong. - The same trail can’t be used more than once.
- The trails of the same mountain can’t be used back-to-back. We must alternate between the 2 mountains.
- The bridge is the only way to move between mountains and it can be used multiple times.
- We can’t start or end on the bridge.
- When we use the bridge, we can’t use it again unless we’ve hiked through a trail first. Hence, when the bridge is used, it must be used before or after using a trail from either mountain.
In the above example, we have these information about the map: n = m = 2, x = 10, A = [40, 45], B = [42, 42], C = 1, D = 100. In total, there are 12 possible hiking routes within the specified range:
- 4 routes which has the length of 40 or 45 (using the trail once then ending the hike).
- 8 routes which has the length of 92 or 97 (using 1 trail from 1 mountain, then move through the bridge, then use 1 more trail from the other mountain, then end the hike).
Our objective is to find the number of hiking routes that can be taken within the specified length range given a map. Below is the example input for our program.
3
3 5 100 245 245
10 20 30
1 2 3 4 5
5 5 1 39 39
1 2 3 4 5
5 4 3 2 1
5 5 1 1 3
1 1 1 1 1
1 1 1 1 1
First, as always, we have the number of test cases T. Each test cases have 3 lines. The first line of a test case include n, m, x, C, and D, respectively. The second line is the A array and the third line is the B array.
Firstly, we need to read the data into our program:
def main():
data = sys.stdin.read().strip().split()
it = iter(data)
T = int(next(it))
for i in range(T):
n, m, x, C, D = [int(next(it)) for i in range(5)]
A = [int(next(it)) for i in range(n)]
B = [int(next(it)) for i in range(m)]
print(solve(n, m, x, C, D, A, B))
if __name__ == "__main__":
main()
Below is my alternating DFS approach to this problem.
from functools import cache
def solve(n, m, x, C, D, A, B):
@cache
def dfs_from_A(used_A, used_B, total_len):
if total_len > D:
return 0 # prune
count = 1 if C <= total_len <= D else 0
# next is B
for i in range(m):
if not (used_B & (1 << i)):
new_length = total_len + x + B[i]
if new_length <= D:
count += dfs_from_B(used_A, used_B | (1 << i), new_length)
return count
@cache
def dfs_from_B(used_A, used_B, total_len):
if total_len > D:
return 0 # prune
count = 1 if C <= total_len <= D else 0
# next is A
for i in range(n):
if not (used_A & (1 << i)):
new_length = total_len + x + A[i]
if new_length <= D:
count += dfs_from_A(used_A | (1 << i), used_B, new_length)
return count
num_routes = 0
for i in range(n):
num_routes += dfs_from_A(1 << i, 0, A[i])
for i in range(m):
num_routes += dfs_from_B(0, 1 << i, B[i])
return num_routes
The problem requires us to alternate between the 2 mountains so I implemented this alternating DFS approach. used_A and used_B are bitmasks that indicates which indices of A and B have already been used in the current route.
For each DFS, we first check if the length of the route is longer than D, if yes then we prune the search branch and return 0 immediately. We set count to 1 if the current partial route is within the C and D range, else we set it to 0.
We loop over the unused trails in the list and calculate the new length with an unused trail. If the new length fits within the range, we call the other DFS function and continue until we run out of trails or we found a route that fits within the range.
Finally, we start the algorithm by working through each route in both A and B, hence the 2 loops at the end of the solve() function. The @cache directive is used to memoize the recursive calls and speed the program up. Although this solution works on the example inputs, it ultimately did not meet the time limit requirement.
Conclusion
I had a lot of fun in this competition as I got to exercise my coding and problem solving skill. Although I didn’t make it to the top 50, I’m still quite happy with my performance. I hope you enjoyed reading my approaches to these 4 problems.
If you want to get into competitive programming, I’d suggest you start practicing on Codeforces and read the Competitive Programmer’s Handbook.