Mô Phỏng Tên Lửa Điều Chỉnh Vectơ Đẩy trong Python
Kĩ thuật tên lửa là 1 topic mà mình rất thích và mình cũng muốn thử build 1 tên lửa mô hình từ rất lâu rồi. Nhưng do nhiều lí do khác nhau, mình không thể build 1 cái tên lửa mô hình được. Thế nên mình sẽ đi theo hướng mô phỏng tên lửa.
Mình sẽ build 1 chương trình mô phỏng cho 1 cái tên lửa điều khiển vectơ đẩy. Loại tên lửa này có thể điều chỉnh hướng phóng của động cơ để thay đổi hướng bay. Tên lưa này sẽ được cấu hình khá giống với thực thế, nó sẽ không giống với thực tế 100%, nhưng đa phần thì nó sẽ giống với thực tế. Mình đã ghi chép lại tất cả chi tiết về dự án này để bất kì ai cũng có thể đọc và học làm theo được.
Note: Mình sẽ không mô phỏng những yếu tố như gió hay lực cản không khí bởi vì nó hơi quá phức tạp cho cái scope của dự án này. Mình cũng sẽ không lập trình PID hay tạo hệ thống điều khiển đóng gì cả. Mình sẽ add các yếu tố và hệ thống điều khiển vào chương trình mô phỏng này trong tương lai.
Đo đạc thông số về tên lửa
1 chỉ số rất quan trọng mà chúng ta sẽ cần để làm mô phỏng là mô men quán tính khối lượng. Mô men quán tính khối lượng có thể được hiểu là độ “kháng lại” của tên lửa với thay đổi về mặt quán tính. Cả khối lượng riêng và sự phân bố khối lượng sẽ làm ảnh hưởng tới mô men quán tính khối lượng.
Mình sẽ giải thích ngắn gọn về các chỉ số đo và cách đo. Nếu như bạn muốn hiểu rõ hơn về chỉ số, cách đo và muốn nhìn minh hoa thì bạn có thể xem video này của BPS space. Mình lấy các chỉ số từ video này luôn bởi vì mình không có cách nào để đo 1 tên lửa mô hình ngoài đời thật.
Để tính mô men quán tính khối lượng thì chúng ta sẽ cần khối lượng của tên lửa (kg). Tên lửa của mình sẽ có khối lượng là $0.543kg$.
Tiếp theo, chúng ta cần chỉ số COM-string, chỉ số này sẽ là $0.3m$, chúng ta cũng cần độ dài của dây treo, chỉ số này sẽ là $0.65m$.
Tiếp theo, chúng ta cũng sẽ cần chỉ số cánh tay đòn của tên lửa. Cánh tay đòn là khoảng cách giữa điểm gắn bộ đẩy và trọng tâm của tên lửa. Chỉ số này sẽ rất quan trọng khi chúng ta cần tính mô men xoắn. Chỉ số cánh tay đòn của mình sẽ là $0.28m$.
Tiếp theo thì chúng ta sẽ cần thời gian trung bình giữa mỗi giao động của tên lửa. Chỉ số thời gian này của mình sẽ là $1.603s$.
Mình chỉ nhắc đến các chỉ số này thôi, nếu như bạn muốn biết chi tiết hơn về các chỉ số này thì bạn có thể xem video của BPS space được nhắc đến ở trên.
Tóm gọn lại thì đây là tất cả các chỉ số chúng ta sẽ cần để tính mô men quán tính khối lượng:
- Trọng lượng của tên lửa: $m = 0.543kg$
- Gia tốc trọng trường: $g = 9.81 m / s^2$
- Thời gian giữa các giao động: $R_t = 1.603s$
- Khoảng cách từ trọng tâm tới dây treo: $d = 0.3m$
- Độ dài của dây treo: $l = 0.65m$
We can then plug these values into the mass moment of inertia equation: Với những chỉ số này, mình có thể sử dụng phương trình mô men quán tính khối lượng:
$$ MMOI = \frac{m * g * R_t^2 * d^2}{4 \pi^2 * l} $$
Mình tính ra được giá trị mô men quán tính khối lượng là $0.048kg \cdot m^2$.
3 bậc tự do
1 tên lửa thường sẽ có 3 bậc tự do (3DOF): pitch, yaw, và roll. Bức ảnh này (từ Wikipedia) cho thấy mỗi bậc tự do là gì trong không gian 3D:
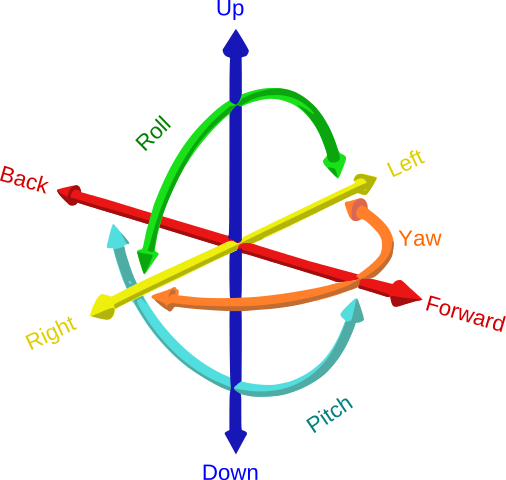
Hàm 3 bật tự do sẽ giúp chúng ta mô phỏng động lực bay của tên lửa bằng cách tính toán sự vận động và góc độ dựa trên lực và mô men được áp đặt lên tên lửa đó. Bởi vì mình đang build chương trình mô phỏng 2D, mình chỉ cần hàm 3DOF có thể tính toán ở trục X và Z.
Chúng ta sẽ cần dữ liệu về lực, mô men, và trọng lượng để có thể mô phỏng động lực của nó. Đầu ra của sẽ là các thông tin đại diện cho trạng thái của tên lửa trong khi nó bay.
Đầu vào của hàm 3DOF:
- Lực tác động ở trục X và Z ($Fx$ và $Fz$)
- Mô men pitch ($My$): Đại diện cho mô men xoắn
Đầu ra của hàm 3DOF:
- Góc pitch ($\theta$): Góc giữa trục tên lửa với mặt phẳng tham chiếu
- Độ thay đổi góc pitch ($q$): Độ thay đổi của góc pitch
- Gia tốc góc pitch ($dqdt$): Độ thay đổi của độ thay đổi của góc pitch
- Tọa độ ($(x, z)$): Tọa độ vị trí của tên lửa
- Vận tốc ($(u, w)$): ận tốc ở trúc X và Z của tên lửa
- Gia tốc ($(Ax, Az)$): Gia tốc của tên lửa
Đây là pitch trong tên lửa:
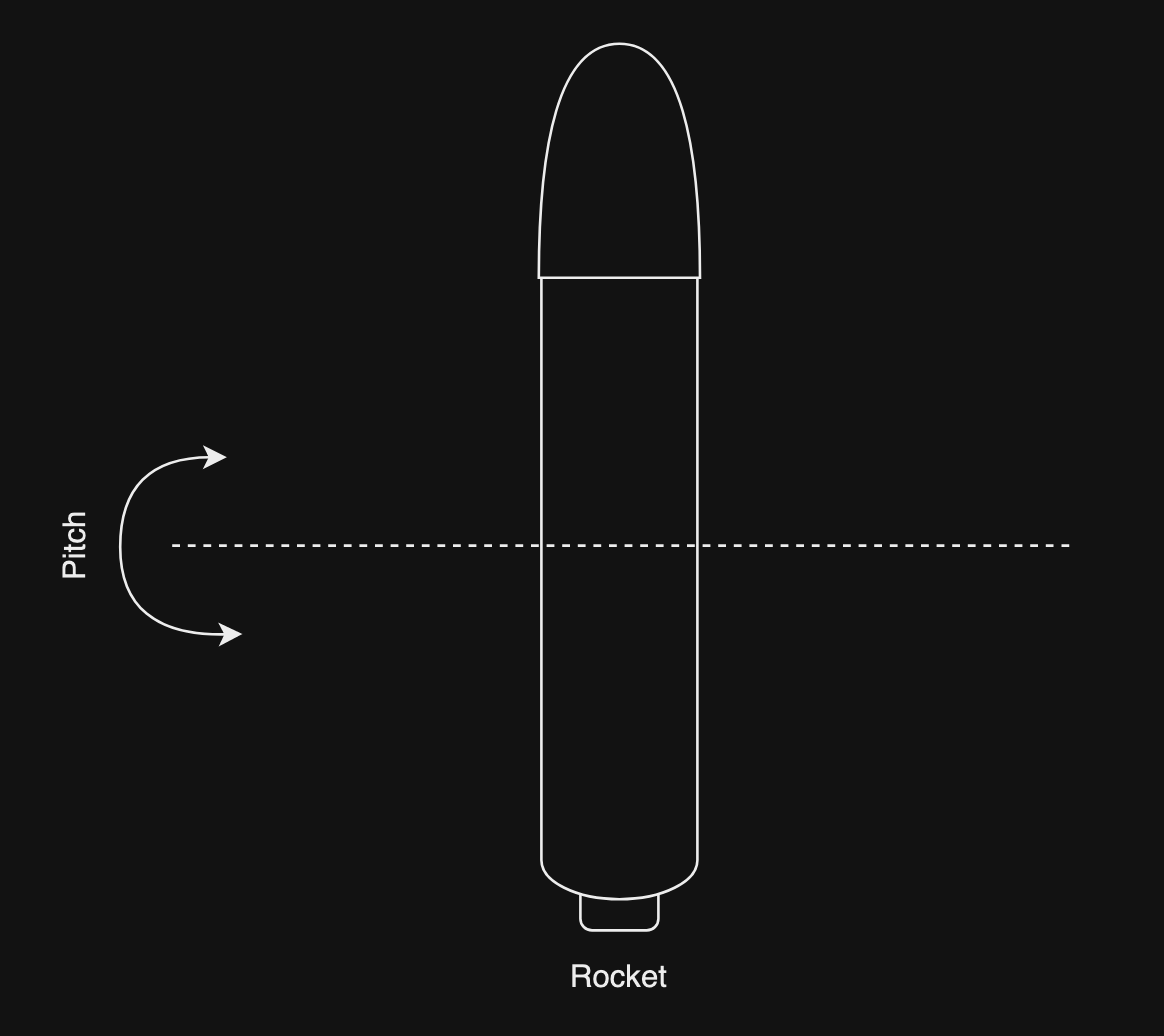
Lập trình hàm 3DOF
Chúng ta sẽ cần thư viện numpy và matplotlib để lập trình:
import numpy as np
import matplotlib.pyplot as plt
Hàm 3DOF sẽ cần thông số của tên lửa khi nó chưa được phóng:
'''
Đầu vào:
- Fx: Lực ở trục X (N)
- Fz: Lực ở trục Z (N)
- My: Mô mem pitch, đại diện cho mô mem xoắn (Nm)
- u0: Vận tốc bắt đầu ở trục X
- w0: Vận tốc bắt đầu ở trục Z
- theta0: Góc pitch bắt đầu
- q0: Độ thay đổi bắt đầu của góc pitch
- pos0: Điểm xuất phát [x, z]
- mass: Trọng lượng
- inertia: Mô men quán tính khối lượng
- g: Gia tốc trọng trường
- dt: Bước nhảy thời gian
- duration: Thời gian mô phỏng
'''
def three_dof_body_axes(Fx, Fz, My, u0=0.0, w0=0.0, theta0=0.0, q0=0.0, pos0=[0.0, 0.0], mass=0, inertia=0.0, g=9.81, dt=0.01, duration=10):
Bước nhảy thời gian ở đây là đại diện cho khoảng thời gian nhỏ mà các phương trình sẽ được thực hiện để tính toán thay đổi trong trạng thái của tên lửa.
Mình sẽ gán các đầu vào này vào 1 biến trong hàm để mình làm việc với các dữ liệu đó dễ hơn:
pos = np.array(pos0, dtype=float) # đảm bảo pos0 là mảng float
u = u0
w = w0
vel = np.array([u, w]) # vận tốc
theta = theta0
q = q0
Chúng ta sẽ cần tính gia tốc đầu bắt đầu của tên lửa ở trục X và Z. Chúng ta có thể sử dụng phương trình $F=ma$ để tính. Ở trục Z thì chúng ta cũng cần trừ gia tốc trọng trường bởi vì trọng lực. Mình sẽ truy cập giá trị lực bắt đầu của 2 trục bằng cách lấy giá trị đầu tiên của Fx và Fz:
ax = Fx[0] / mass
az = Fz[0] / mass - g
Mình sẽ tạo ra 1 vài mảng để giữ các dữ liệu trạng thái ở mỗi khoảng thời gian nhỏ $dt$:
theta_list = [theta]
q_list = [q]
dqdt_list = [0]
pos_list = [pos.copy()]
velocity_list = [vel.copy()]
acceleration_list = [np.array([ax, az])]
Bởi vì chúng ta thực chất là đang giải 1 đống phương trình vi phần thường (ODE), chúng ta có thể dùng phương pháp Euler để giải các phương trình này và cập nhật các biến trạng thái trong mảng đầu ra:
# tích phân theo thời gian bằng phương pháp Euler
for t in np.arange(dt, duration + dt, dt): # bắt đầu ở dt và kết thúc ở duration
Vòng lặp này cho phép chúng ta tính toán và dùng phương trình ở mỗi thời điểm $dt$, là khoảng $0.01s$.
Chúng ta cũng cần tính gia tốc tức thì ở trục X và Z tại thời điểm $dt$:
# tính gia tốc
ax = Fx[int(t/dt)] / mass
az = Fz[int(t/dt)] / mass - g
Chúng ta có thể tính toán gia tốc góc pitch bằng cách chia mô men xoắn với mô men quán tính khối lượng. Bạn có thể nghĩ nó như là chia mô men xoắn với độ “kháng lại” thay đổi với quán tính:
# tính gia tốc góc pitch
dqdt = My[int(t/dt)] / inertia
Chúng ta cũng cần tính vận tốc X và Z, độ thay đổi của góc pitch, vị trí và góc pitch tại thời điểm $dt$ có tính đến các trạng thái trước đó. Cách tính này sẽ cho phép chúng ta mô phỏng cách mà động lực của tên lửa sẽ thay đổi theo thời gian:
# tính vận tốc và độ thay đổi của góc pitch
u += ax * dt
w += az * dt
q += dqdt * dt
# tính vị trí
pos += vel * dt
vel = np.array([u, w])
# tính góc pitch
theta += q * dt
Sau khi tính toán thì chúng ta sẽ cần lưu lại các giá trị này vào trong mảng đầu ra:
theta_list.append(theta)
q_list.append(q)
dqdt_list.append(dqdt)
pos_list.append(pos.copy())
velocity_list.append(vel.copy())
acceleration_list.append(np.array([ax, az]))
Chúng ta cũng sẽ cần 1 điều khiện ngừng để tính đến trường hợp tên lửa đâm vào mặt đất. Chúng ta có thể check xem giá trị vị trí ở trục Z có nhỏ hơn hoặc bằng 0 ở thời điện hiện tại hay ko. Chúng ta cũng cần đợi khoảng 2 giây để tên lửa có thể phóng lên từ vị trí 0:
if pos[1] <= 0 and t > 2:
break
Đó là cách lập trình hàm 3DOF. Đây là code full của hàm đó:
def three_dof_body_axes(Fx, Fz, My, u0=0.0, w0=0.0, theta0=0.0, q0=0.0, pos0=[0.0, 0.0], mass=0, inertia=0.0, g=9.81, dt=0.01, duration=10):
pos = np.array(pos0, dtype=float)
u = u0
w = w0
theta = theta0
q = q0
vel = np.array([u, w])
ax = Fx[0] / mass
az = Fz[0] / mass - g
theta_list = [theta]
q_list = [q]
dqdt_list = [0]
pos_list = [pos.copy()]
velocity_list = [vel.copy()]
acceleration_list = [np.array([ax, az])]
for t in np.arange(dt, duration + dt, dt):
ax = Fx[int(t/dt)] / mass
az = Fz[int(t/dt)] / mass - g
dqdt = My[int(t/dt)] / inertia
u += ax * dt
w += az * dt
q += dqdt * dt
pos += vel * dt
vel = np.array([u, w])
theta += q * dt
theta_list.append(theta)
q_list.append(q)
dqdt_list.append(dqdt)
pos_list.append(pos.copy())
velocity_list.append(vel.copy())
acceleration_list.append(np.array([ax, az]))
if pos[1] <= 0 and t > 2:
break
return {
'theta' : np.array(theta_list),
'q' : np.array(q_list),
'dqdt' : np.array(dqdt_list),
'pos' : np.array(pos_list),
'velocity' : np.array(velocity_list),
'acceleration' : np.array(acceleration_list)
}
Đặc tính lực đẩy
Chúng ta sẽ cần 1 mảng chứa đặc tính lực đẩy. Đặc tính lực đẩy là lực đẩy của tên lửa ở 1 khoảng thời gian nhất định. Tên lửa chúng mình có lực đẩy max là $15N$. Chúng ta sẽ mô phỏng 4 giai đoạn đẩy mà tên lửa mô hình thường có:
4 giai đoạn đẩy này sẽ là giai đoạn tăng tốc, giai đoạn max lực đẩy, giai đoạn giảm tốc, và giai đoạn burnout.
- Giai đoạn tăng tốc: Ở giai đoạn này, tên lửa sẽ nhanh chóng tăng lực đẩy từ $0N$ lên $15N$. Giai đoạn này chiếm khoảng $10%$ thời gian đẩy. Chúng ta có thể mô phỏng giai đoạn này qua phương trình bậc 2, nó cho phép tên lửa của mình bắt đầu dần dần tăng nhanh lên trong 1 khoảng thời gian nhất định.
- Giai đoạn max lực đẩy: Ở giai đoạn này, tên lửa sẽ có lực đẩy là max $15N$. Giai đoạn này sẽ chiếm khoảng $20%$ thời gian đẩy.
- Giai đoạn giảm tốc: Ở giai đoạn này, tên lửa sẽ dần dần giảm tốc từ $15N$ xuống $0N$. Giai đoạn này sẽ chiếm khoảng $70%$ thời gian đẩy. Chúng ta có thể mô phỏng giai đoạn này với 1 phương trình tuyến tính.
- Burnout: Ở giai đoạn này, tên lửa sẽ có lực đẩy là $0N$. Giai đoạn này sẽ xảy ra sau thời gian đẩy.
Lập trình hàm tạo đặc tính lực đẩy
Hàm tạo này sẽ cần thời gian mô phỏng, thời gian đẩy, lực đẩy max, và khoảng thời gian bước $dt$:
def generate_thrust_profile(duration, thrust_duration, peak_thrust, dt=0.01):
Chúng ta sẽ cần tính lực đẩy của tên lửa ở mỗi khoảng thời gian từ 0 đến hết thời gian đẩy. Chúng ta sẽ lưu giá trị lực đẩy này vào 1 mảng đặc tính lực đẩy:
thrust_profile = []
for t in np.arange(0, duration + dt, dt):
Đầu tiên thì mình sẽ lập trình giai đoạn tăng tốc ($10%$ thời gian đẩy):
if t < 0.1 * thrust_duration:
thrust = peak_thrust * (10 * t / thrust_duration)**2
Đây là phương trình bậc 2. Mình nhân 10 với t / thrust_duration để chuẩn hóa dữ liệu vào khoảng $[0, 1]$ (đây là phần trăm thời gian đã trôi qua). Rồi mình dùng căn bậc 2 và nhân với peak_thrust để tính giá trị đẩy ở thời điểm $t$. Phương trình này sẽ tạo ra 1 đặc tính lực đẩy tăng chậm ban đầu rồi tăng nhanh dần dần.
Tiếp theo thì mình sẽ lập trình giai đoạn max lực đẩy ($20%$ thời gian đẩy):
elif t < 0.3 * thrust_duration:
thrust = peak_thrust
Giai đoạn này sẽ kết thục vào khoảng $30%$ của thời gian đẩy (bởi vì giai đoạn tăng tốc đã chiếm $10%$ rồi).
Tiếp theo thì mình sẽ lập trình giai đoạn giảm tốc ($70%$ thời gian đẩy)
elif t < thrust_duration:
thrust = peak_thrust * (1 - (t - 0.3 * thrust_duration) / (0.7 * thrust_duration))
Đây là phương trình tuyến tính. Mình sẽ giải thích từng đoạn:
((t - 0.3 * thrust_duration) / (0.7 * thrust_duration))
(t - 0.3 * thrust_duration) sẽ cho chúng ta biết thời gian đã qua kể từ kết thúc của giai đoạn max lực đẩy. Sau đó chia với (0.7 * thrust_duration) sẽ cho chúng ta biết được phần trăm của thời gian hiện tại ở trong khoảng $70%$ của giai đoạn giảm tốc. Chúng ta sẽ biết được chúng ta ở trong giai đoạn giảm tốc lâu đến đâu.
(1 - (t - 0.3 * thrust_duration) / (0.7 * thrust_duration))
Bởi vì chúng ta muốn lực đẩy dần dần giảm, chúng ta sẽ trừ với 1 để đảo ngược giá trị phần trăm chúng ta vừa tính được. Và cuối cùng thì chúng ta có thể nhân nó với giá trị lực đẩy max.
Tiếp theo thì mình sẽ lập trình giai đoạn burnout:
else:
thrust = 0
Cuối cùng thì mình sẽ cho giá trị tính được vào 1 mảng đầu ra, và quay lại vòng lặp. Đó là hàm tạo đặc tính lực đẩy. Đây là code full của hàm:
def generate_thrust_profile(duration, thrust_duration, peak_thrust, dt=0.01):
thrust_profile = []
for t in np.arange(0, duration + dt, dt):
if t < 0.1 * thrust_duration:
thrust = peak_thrust * (10 * t / thrust_duration)**2
elif t < 0.3 * thrust_duration:
thrust = peak_thrust
elif t < thrust_duration:
thrust = peak_thrust * (1 - (t - 0.3 * thrust_duration) / (0.7 * thrust_duration))
else:
thrust = 0
thrust_profile.append(thrust)
return np.array(thrust_profile)
Mình sẽ dùng hàm này để tạo ra 1 đặc tính lực đẩy và mình sẽ vẽ lược đồ cho đặc tính này:
# giá trị
peak_thrust = 15 # N
thrust_duration = 4 # s
simulation_duration = 30 # s
dt = 0.01 # s
# tạo đặc tính
thrust_profile = generate_thrust_profile(simulation_duration, thrust_duration, peak_thrust, dt)
time_range = np.arange(0, simulation_duration + dt, dt)
# vẽ lược đồ
plt.figure(figsize=(10, 6))
plt.plot(time_range, thrust_profile, label='Thrust')
plt.axvline(x=0.1 * thrust_duration, color='red', linestyle='--', label='End of rapid rise')
plt.axvline(x=0.3 * thrust_duration, color='green', linestyle='--', label='End of peak thrust')
plt.axvline(x=thrust_duration, color='orange', linestyle='--', label='End of decay phase (Burnout)')
plt.xlabel('Time (s)')
plt.ylabel('Thrust (N)')
plt.title('Thrust Profile')
plt.legend()
plt.grid()
plt.show()
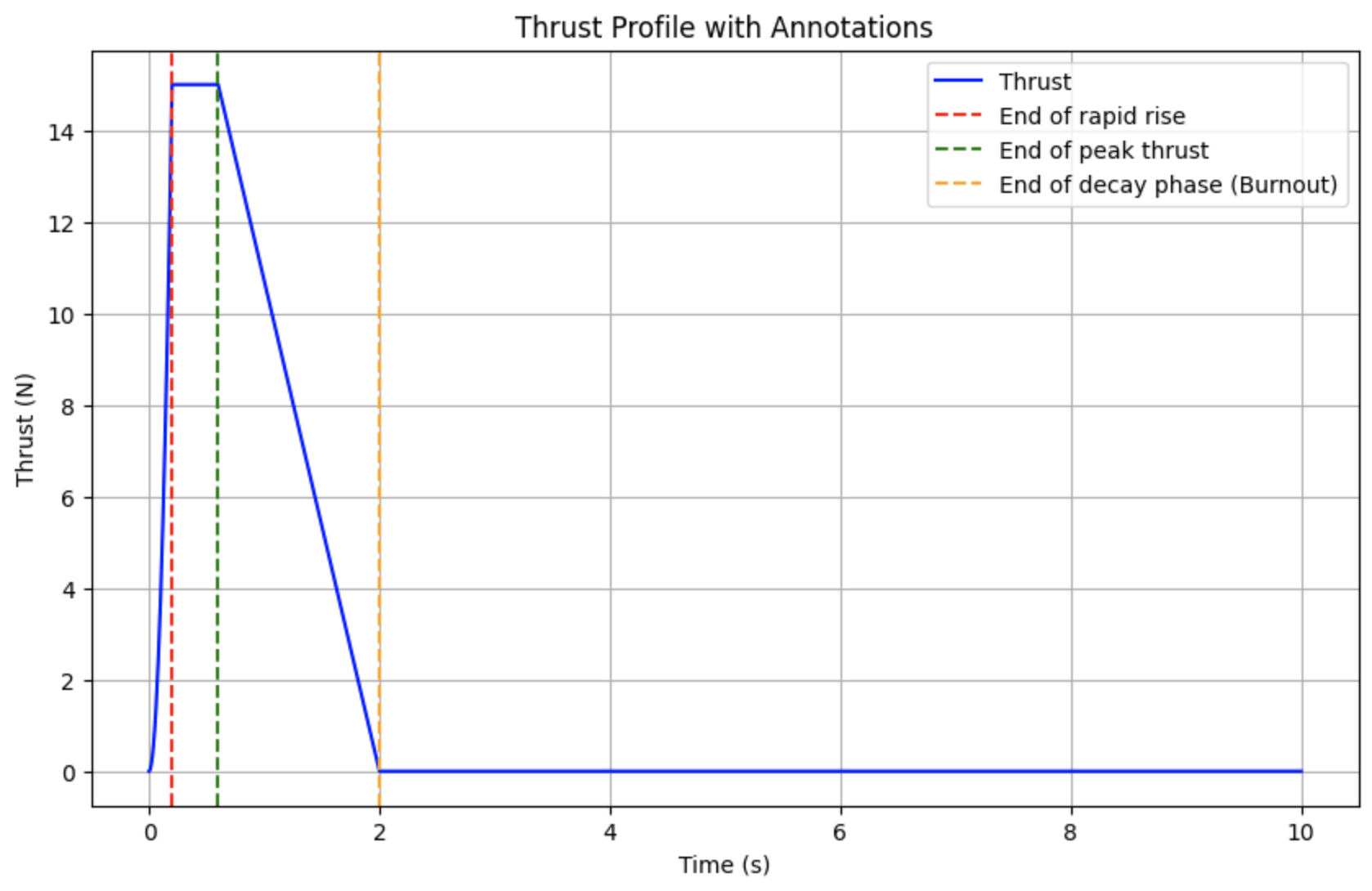
Chúng ta có thể thấy là giai đoạn tăng tốc bắt đầu chậm nhưng tăng tốc lên rất nhanh, giai đoạn max lực đẩy là 1 hằng số, và giai đoạn giảm tốc là tuyến tính. Thế là hàm của chúng ta hoạt động tốt.
Chúng ta có thể sử dụng hàm tạo đặc tính lực đẩy này để tính động lực của tên lửa và mô phỏng nó.
Mô phỏng tên lửa
Chúng ta sẽ cần tạo 1 số tham số và điều kiện bắt đầu của tên lửa. Mình sẽ đặt thời gian mô phỏng là 30 giây:
# tham số
mass = 0.543 # kg
inertia = 0.048 # kg*m^2
g = 9.81 # m/s^2
peak_thrust = 15 # N
thrust_duration = 4 # s
simulation_duration = 30 # s
dt = 0.01 # s
moment_arm = 0.28 # mét
gimbal_angle = 0.00 # radian
# điều kiện bắt đầu
u0 = 0.0 # vận tốc ban đầu x
w0 = 0.0 # vận tốc ban đầu z
theta0 = 0.0 # góc pitch ban đầu
q0 = 0.0 # độ thay đổi góc pitch ban đầu
pos0 = [0.0, 0.0] # vị trí ban đầu [x, z]
# tạo đặc tính lực đẩy
thrust_profile = generate_thrust_profile(simulation_duration, thrust_duration, peak_thrust, dt)
Note: biến gimbal_angle được đặt với giá trị là $0rad$. Đây là góc của gimbal của động cơ đẩy. Chúng ta sẽ có thể thấy được nếu như thay đổi giá trị này thì tên lửa sẽ ra sao trong 1 lúc nữa. Hiện tại thì mình sẽ đặt nó về 0, tức là tên lửa sẽ bắn thẳng lên trời.
Tiếp theo thì chúng ta sẽ cần tính lực ở trục X và Z cùng với mô men xoắn dựa trên đặc tính lực đẩy:
Fx = np.sin(gimbal_angle) * thrust_profile # lực ngang
Fz = np.cos(gimbal_angle) * thrust_profile # lực dọc
My = Fx * moment_arm # mô men pitch (mô men xoắn)
Mình sử dụng 1 vài phương trình lượng giác để tính lực đẩy của tên lửa trên 2 trục. Đây là cách tính của mình:
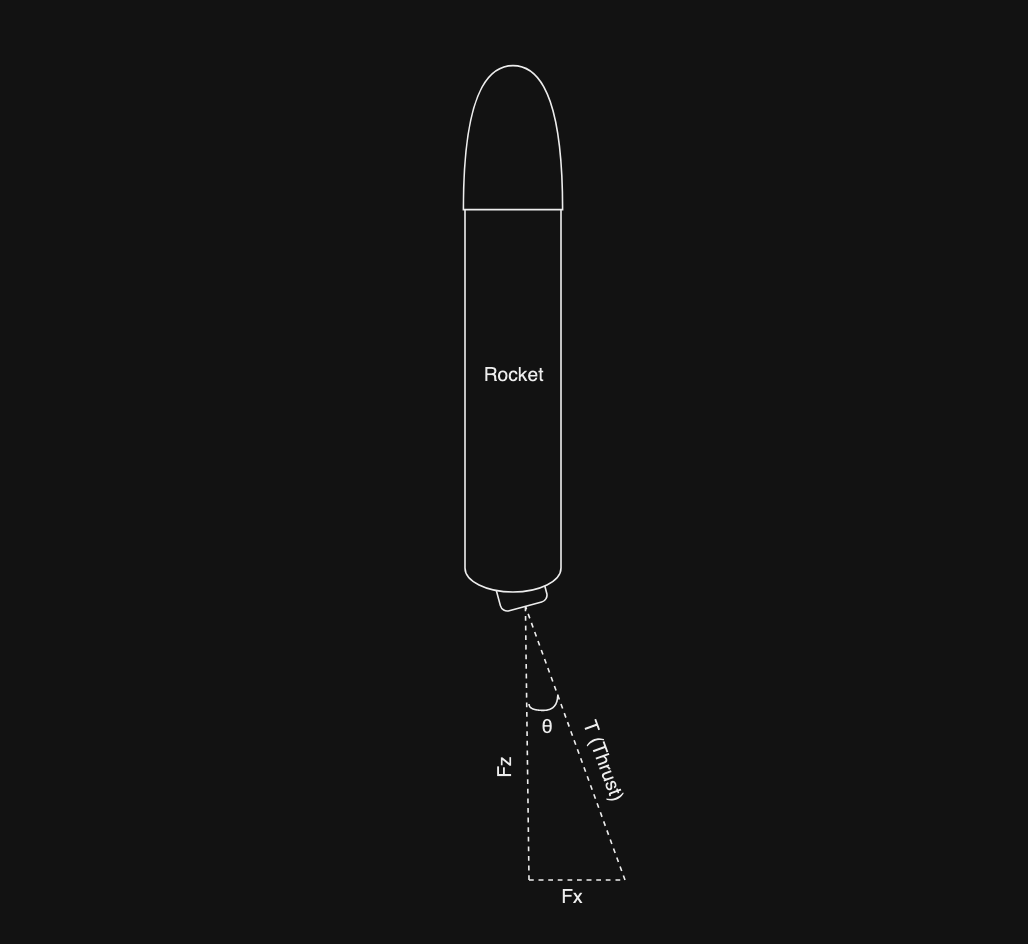
Đây là cách mà lực $F_x$ và $F_z$ được áp đặt lên tên lửa, với $\theta$ là góc gimbal. Chúng ta có thể thấy được với tam giác vuông này thì chúng ta có thể áp dụng những phương trình lượng giác để tính được $F_x$ và $F_z$:
$$ \sin(\theta) = \frac{F_x}{T}, \ \cos(\theta) = \frac{F_z}{T} $$
Sắp xếp lại 2 phương trình này sẽ cho ra 2 phương trình dùng để tính $F_x$ và $F_z$:
$$ F_x = \sin(\theta) * T, \ F_z = \cos(\theta) * T $$
Với mô men xoắn thì chúng ta có thể nhân lực $F_x$ với giá trị cánh tay đòn bởi vì lực đẩy ngang sẽ tạo ra mô men quanh trọng tâm của tên lửa (nó được dùng để điều khiển pitch, thế nên nó được gọi là mô men pitch).
Đây là tất cả các giá trị mà chúng ta cần để cho vào hàm 3DOF:
results = three_dof_body_axes(Fx, Fz, My, u0, w0, theta0, q0, pos0, mass, inertia, g, dt, simulation_duration)
time = np.arange(0, len(results['pos']) * dt, dt)
pos = results['pos']
velocity = results['velocity']
acceleration = results['acceleration']
Vẽ lược đồ dữ liệu mô phỏng (góc gimbal = 0)
Mình sẽ vẽ lược đồ cho các giá trị về trạng thái của tên lửa vừa được tính toán:
# vẽ lược đồ (dữ liệu trục Z)
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(time, pos[:, 1], label='Z Position')
plt.xlabel('Time (s)')
plt.ylabel('Z Position (m)')
plt.title('Z Position Data')
plt.legend()
plt.grid()
plt.subplot(3, 1, 2)
plt.plot(time, velocity[:, 1], label='Z Velocity')
plt.xlabel('Time (s)')
plt.ylabel('Z Velocity (m/s)')
plt.title('Z Velocity Data')
plt.legend()
plt.grid()
plt.subplot(3, 1, 3)
plt.plot(time, acceleration[:, 1], label='Z Acceleration')
plt.xlabel('Time (s)')
plt.ylabel('Z Acceleration (m/s^2)')
plt.title('Z Acceleration Data')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
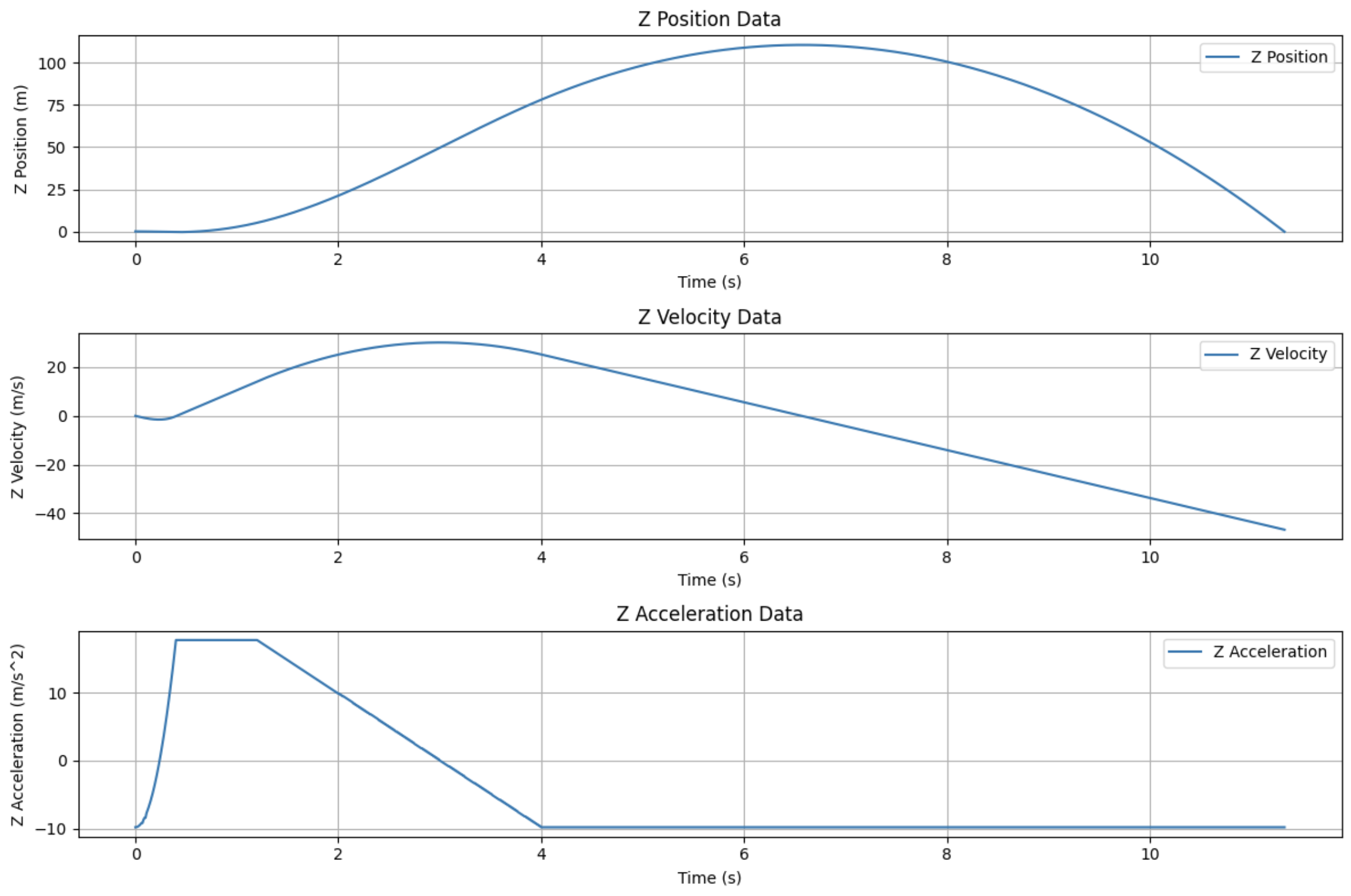
Chúng ta có thể thấy là tên lửa này có thể đạt độ cao khoảng hơn $100m$ với vận tốc tối đa là khoảng $30m/s$. Gia tốc của tên lửa bắt đầu ở khoảng $-9.81m/s^2$ bởi vì tên lửa bị kéo xuống bởi trọng lực. Vào khoảng vài mili giây sau khi phóng thì gia tốc đạt $0m/s^2$, có nghĩa là lực đẩy của tên lửa đã hóa với lực kéo của trọng lực. Vào khoảng vài mili giây sau đó thì nó đạt được gia tốc khoảng $15m/s^2$, rồi nó dần giảm xuống do tên lửa đã vào giai đoạn giảm tốc.
Mình sẽ vẽ lược đồ cho dữ liệu ở trục X:
# vẽ lược đồ (dữ liệu trục X)
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(time, pos[:, 0], label='X Position')
plt.xlabel('Time (s)')
plt.ylabel('X Position (m)')
plt.title('X Position Data')
plt.legend()
plt.grid()
plt.subplot(3, 1, 2)
plt.plot(time, velocity[:, 0], label='X Velocity')
plt.xlabel('Time (s)')
plt.ylabel('X Velocity (m/s)')
plt.title('X Velocity Data')
plt.legend()
plt.grid()
plt.subplot(3, 1, 3)
plt.plot(time, acceleration[:, 0], label='X Acceleration')
plt.xlabel('Time (s)')
plt.ylabel('X Acceleration (m/s^2)')
plt.title('X Acceleration Data')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
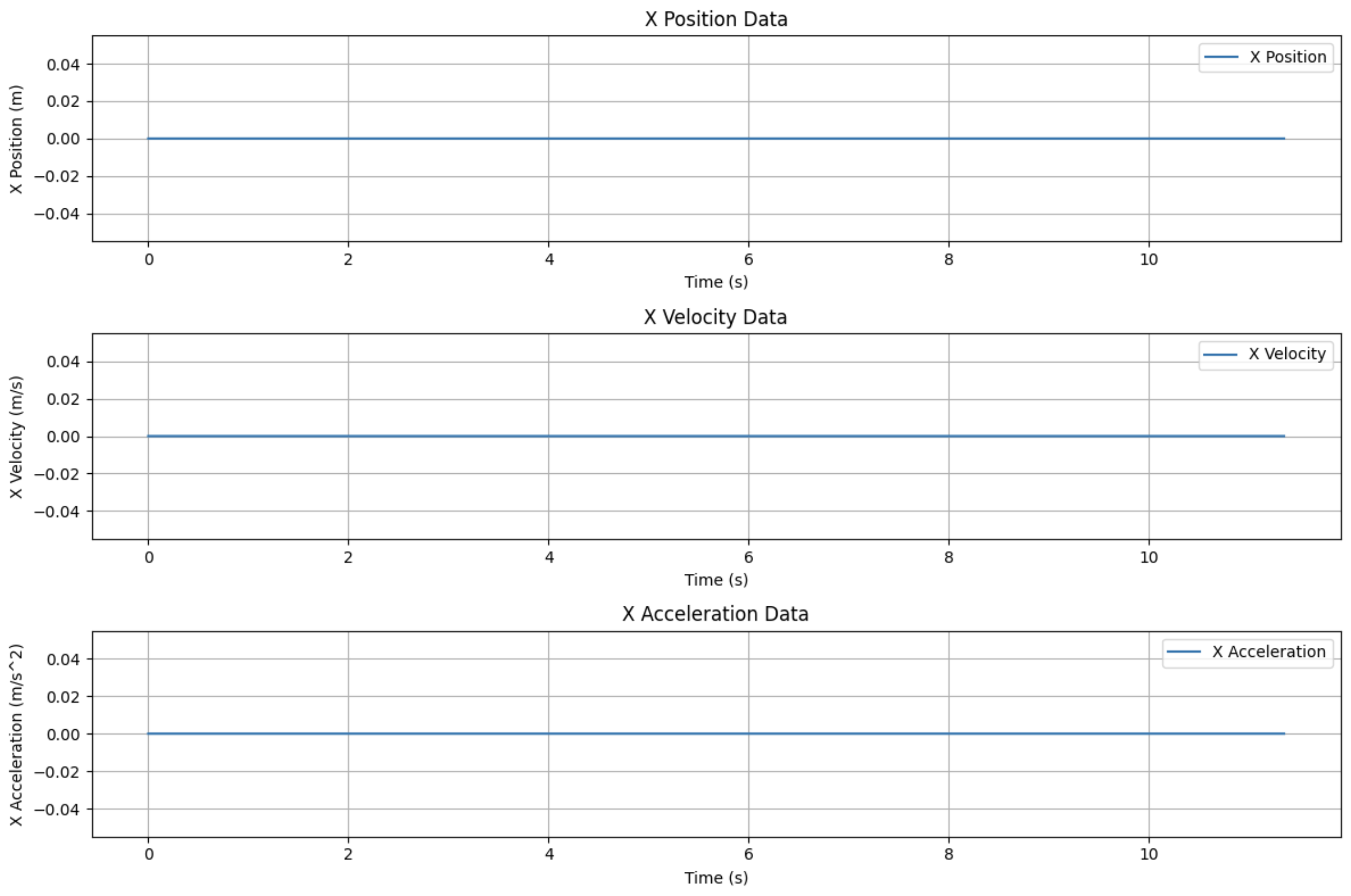
Bởi vì mình đã đặt biến gimbal_angle về $0rad$, tên lửa này sẽ phóng thẳng lên, không di chuyển 1 ít nào ở trục X.
Mình sẽ vẽ lược đồ miêu tả quỹ đạo bay của tên lửa để xem tên lửa này sẽ bay thế nào:
# plot trajectory of rocket (2D) lược đồ quy đạo bay của tên lửa (2D)
plt.figure(figsize=(8, 5))
plt.plot(pos[:, 0], pos[:, 1], label='Rocket Trajectory', color='blue')
plt.scatter(pos[0, 0], pos[0, 1], color='green', label='Launch Point') # điểm xuất phát
plt.scatter(pos[-1, 0], pos[-1, 1], color='red', label='Impact Point') # điểm dừng
plt.axhline(0, color='black', linestyle='--', label='Ground') # mặt đất
plt.xlabel('X Position (m)')
plt.ylabel('Z Position (m)')
plt.title('Rocket Trajectory')
plt.legend()
plt.show()
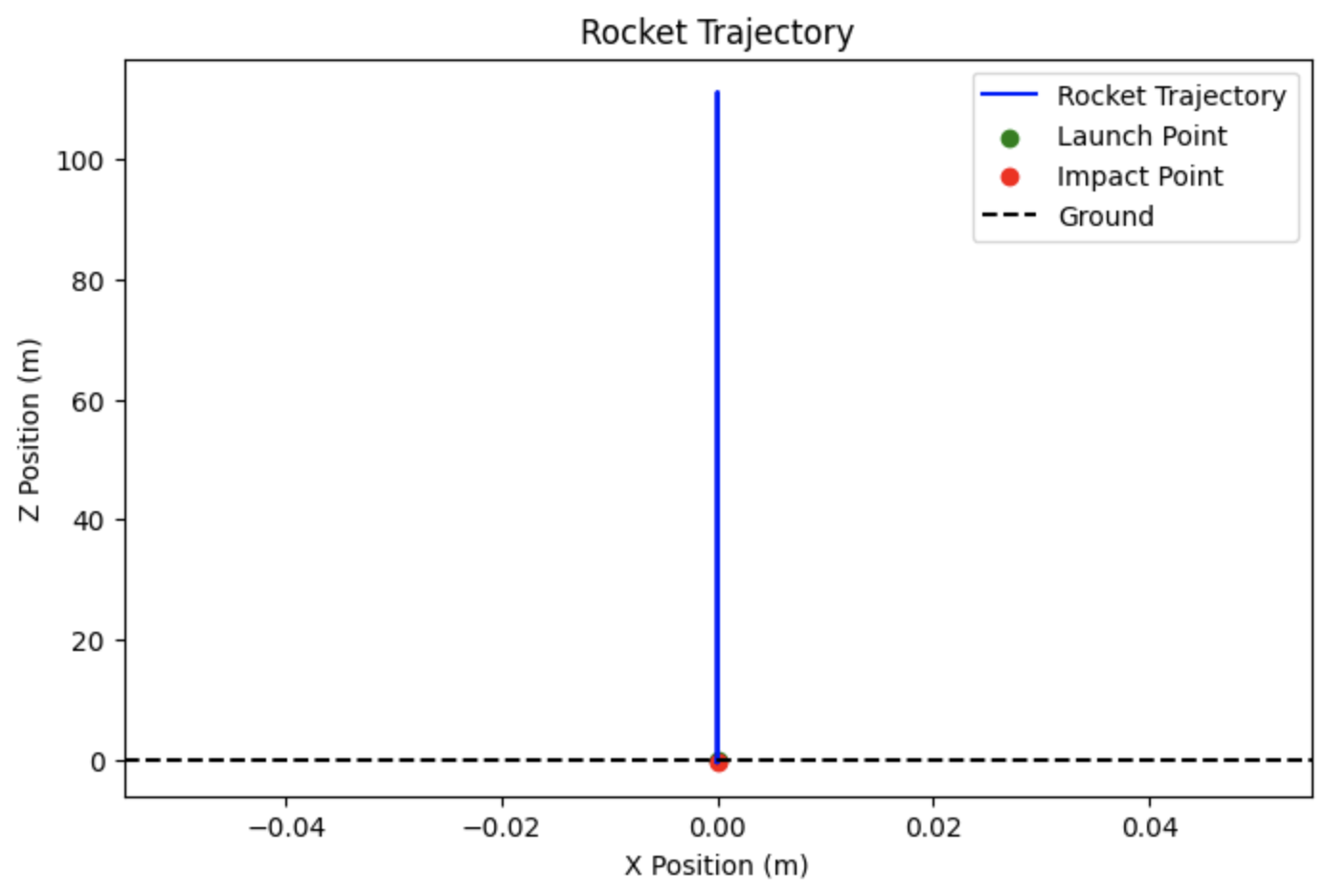
Tên lửa này sẽ phóng thẳng lên khoảng hơn $100m$ 1 ít rồi rơi thẳng xuống.
Vẽ lược đồ dữ liệu mô phỏng (góc gimbal khác 0)
Mình sẽ điều chính góc gimbal để xem tên lửa này sẽ bay thế nào:
gimbal_angle = -0.05 # radian
Và mình sẽ chạy lại chương trình và lấy dữ liệu đầu ra.
- Dữ liệu trục Z:
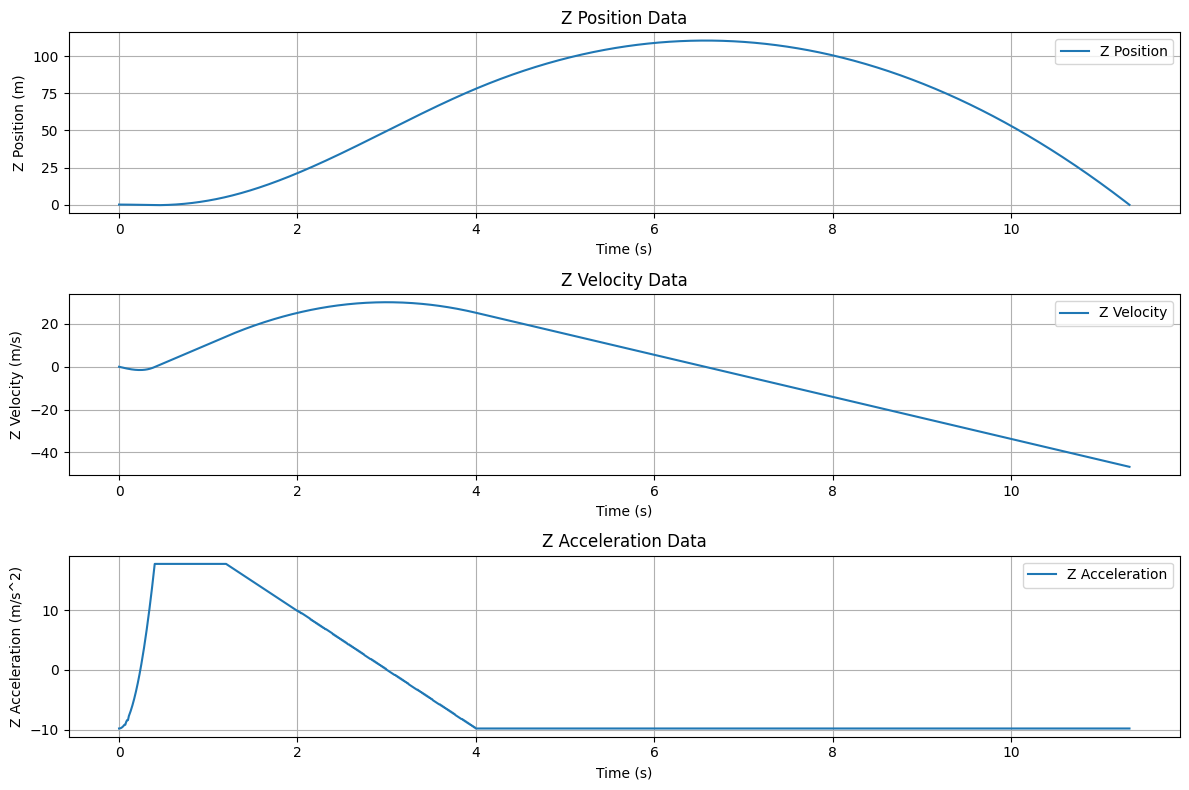
- Dữ liệu trục X:
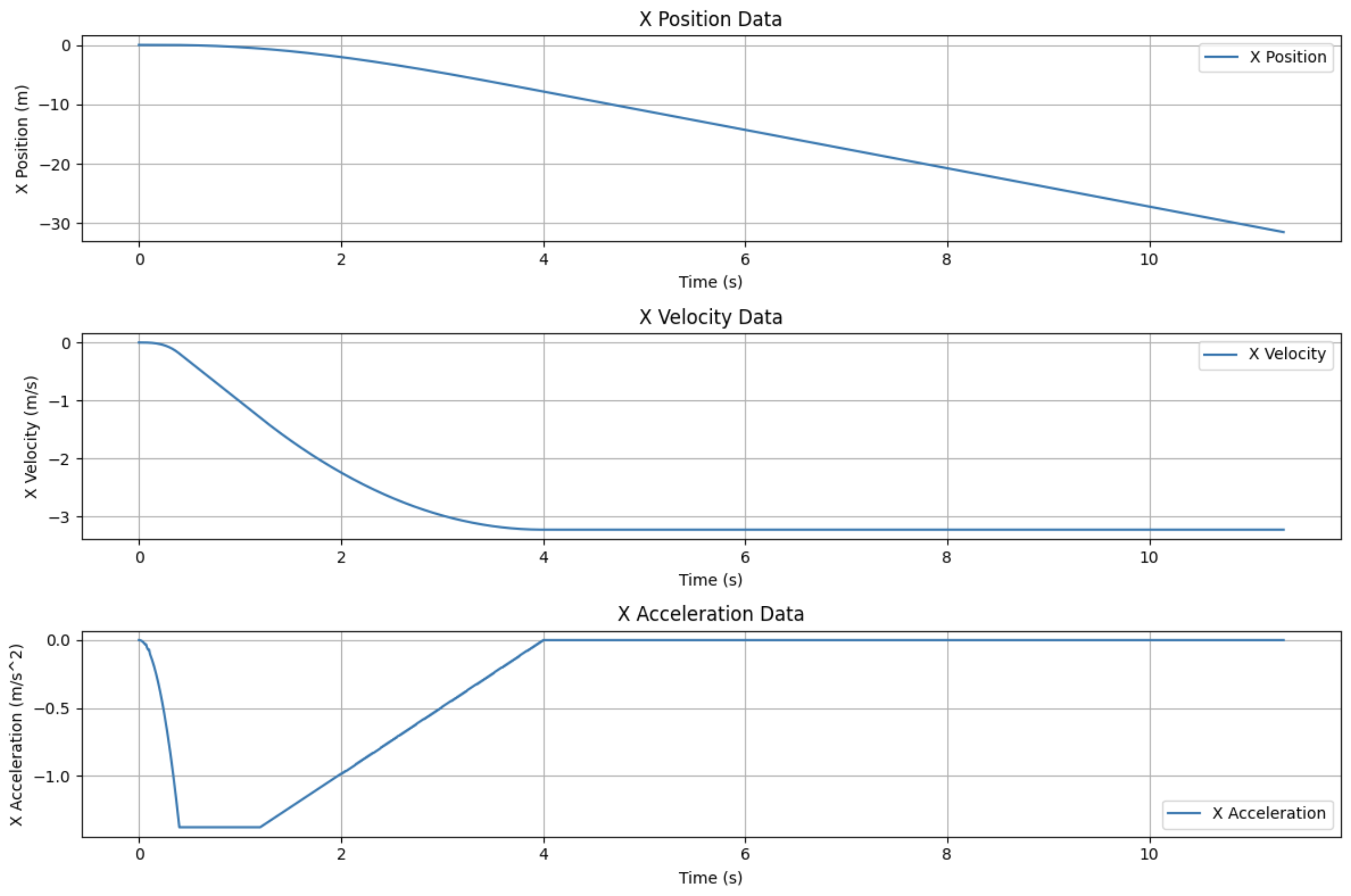
Chúng ta có thể thấy là dữ liệu trục Z không thay đổi từ lần mô phỏng trước, nhưng dữ liệu trục X thay đổi rất nhiều. Dữ liệu vị trí trục X dần dần tiến tới 1 giá trị khác. Điều này có nghĩa là tên lửa đang di chuyển trên trục X. Chúng ta cũng có thể thấy là dữ liệu vận tốc đang giảm xuống giá trị âm do chúng ta đang phóng tên lửa sang bên trái.
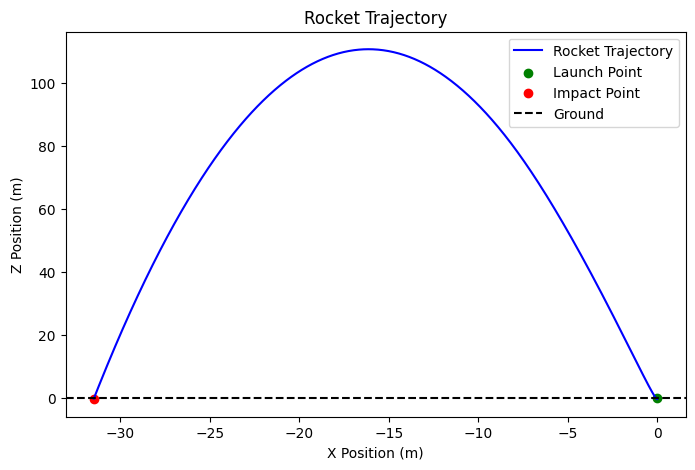
Đây là quỹ đạo của tên lửa này. Chúng ta có thể thấy là tên lửa này bay lên hơn $100m$ và hạ cánh tại vị trí cách vị trí bắt đầu khoảng $30m$. Chúng ta đã mô phỏng tên lửa điều chỉnh vectơ đẩy trong Python thành công.
Kết luận
Chúng ta đã xây dựng 1 chương trình mô phỏng tên lửa điều chỉnh vectơ đẩy trong Python với 3 bậc tự do. Chúng ta cũng đã nói đến 3 bậc tự do là gì, đặc tính lực đẩy là gì, cách lập trình mô phỏng tên lửa và vẽ lược đồ dữ liệu tên lửa và lược đồ quỹ đạo bay của tên lửa.
Dự án này vẫn còn nhiều việc để làm như là lập trình 1 đặc tính lực đẩy giống thực tế hơn, lập trình các yếu tố bên ngoài như là gió hay lực cản không khí, và lập trình 1 bộ điều khiển như là PID để điều khiển tên lửa này. Mình sẽ lập tình các tính năng này vào chương trình mô phỏng này trong tương lai.
Đây là 1 dự án rất hay đối với mình. Mình đã học được thêm rất nhiều thứ về kĩ thuật tên lửa và mình mong rằng bạn cũng đã học thêm được về kĩ thuật tên lửa và động lực tên lửa từ bài đăng blog này.
Tất cả code trong bài đăng này được host tại đây